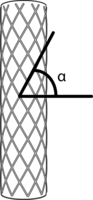
This section describes a Finite Element Method (FEM) model for a particular type of fiber-reinforced actuator using the Abaqus software suite. This actuator differs from the fiber-reinforced actuators discussed in the rest of the documentation, as it consists of a cylindrical elastomeric tube, with circular cross section, and with fibers wrapped in a helical pattern around the outside of the tube. The fibers constrain the motion of the actuator, as they have a much higher stiffness than the elastomer. The angle between the fibers and the horizontal is referred to as the fiber angle α.
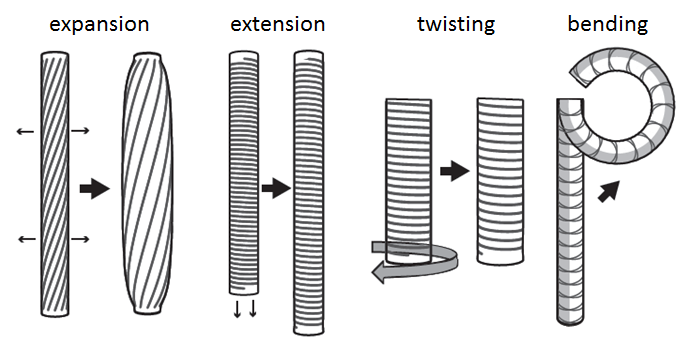
When pressurized, this type of actuator is capable of four types of motion: radial expansion, axial extension, twisting about its axis, or bending. When the elastomeric tube is of uniform stiffness, some combination of expansion, extension, and twisting occurs upon pressurization. When the elastomeric tube is made of two different materials (with different stiffnesses), pressurization produces a bending motion.
The effect of the fiber angle on the behavior of extending, expanding, twisting actuators is illustrated in the video below.
This tutorial describes the procedure for creating an Abaqus model of a fiber-reinforced actuator which extends, expands, or twists upon pressurization. The Abaqus cae file created in this tutorial can be downloaded here: FR_tutorial.cae. To create a model of a bending actuator, follow the main tutorial, and take note of the alternative steps in italics, which describe the modifications which need to be made to produce a bending actuator.
Overview of model components
- A Fluid-Structure Interaction (FSI) problem treated with a standard/implicit FEM using Abaqus/CAE (SIMULIA, Dassault Systèmes)
- Materials:
- Elastosil M4601 silicone rubber: neo-Hookean strain energy potential defined by the coefficient C10 = 0.12MPa.
- Kevlar fiber: elastic material with Young’s modulus 31067MPa and Poisson’s ratio 0.36.
- For a bending actuator:
- Dragon Skin 10 silicone rubber: neo-Hookean strain energy potential defined by the coefficient C10 = 0.0425MPa.
- Smooth-Sil 950 silicone rubber: neo-Hookean strain energy potential defined by the coefficient C10 = 0.34MPa.
- Kevlar fiber: elastic material with Young’s modulus 31067MPa and Poisson’s ratio 0.36.
- Sections:
- Elastosil (uniform solid), assigned to the main body and caps
- Kevlar assigned to the fibers
- For a bending actuator:
- Smooth-Sil 950 (uniform solid), assigned to half of the main body and to the caps
- Dragon Skin 10 (uniform solid), assigned to half of the main body
- Kevlar assigned to the fibers
- 1 load:
- Pressure, acting at all internal faces of the actuator cavity
- Tie constraints between the fibers and the outer wall of the actuator
Overview of FEM steps
- Create parts
- Elastomeric tube and caps
- Fibers
- Create and assign materials
- Create surfaces and loads
- Create surface for applying pressure
- Create step
- Define boundary conditions
- Apply load
- Mesh the parts
- Add tie constraint
- Run job and view results
Scripting in Abaqus
More advanced users of Abaqus may note that all of the above can be done using the scripting interface. For a useful introduction to the Abaqus scripting interface see learnabaqusscriptinonehour.pdf. The scripts corresponding to the model developed in this tutorial can be downloaded here: FR_ACTUATOR.py and PARAMETERS.py. To run the script (equivalent to creating the model and running the job), go to File-> Run script, and browse to the file FR_ACTUATOR.py.
Acknowledgements and References
The content of this tutorial is based on the following work:
- F. Connolly, P. Polygerinos, C. J. Walsh, and K. Bertoldi. “Mechanical programming of soft actuators by varying fiber angle” Soft Robotics, 2015 vol 2 pp 26-32.
Many research groups have worked on this type of actuator, and further interesting references include:
- G Krishnan, J Bishop-Moser, C Kim, and S Kota, "Kinematics of a generalized class of pneumatic artificial muscles", J Mech Robot 2015 doi:10.1115/1.4029705
- S Hirai, P Cusin, H Tanigawa, T Masui, S Konishi and S Kawamura, "Qualitative synthesis of deformable cylindrical actuators through constraint topology" IROS 2000 pp. 197-202
- K Suzumori, S Iikura, and H Tanaka, "Flexible microactuator for miniature robots", Proceedings of Micro Electro Mechanical Systems 1991 pp. 204-209
| learnabaqusscriptinonehour.pdf | 257 KB | |
| fr_scripts.zip | 14 KB | |
| fr_tutorial.zip | 986 KB |
