Smart Braids work by creating a structure that changes inductance over the course of the actuator stroke. For McKibben Muscles, the change in inductance can be modeled with the long solenoid approximation. For more accurate results, or for other types of fiber-reinforced actuators, the Neumann formula can be integrated.
Long Solenoid Approximation
Each right-handed helix of the Smart Braid is connected to an adjacent left-handed helix. In this configuration, the current moves up the actuator along one hand of helix and down the actuator along the other hand. The current always circles the axis of the actuator in the same direction like a solenoid. This allows us to use the Long Solenoid equation to predict the change in inductance.
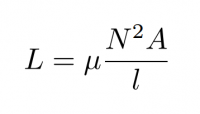
As McKibben Muscles contract, their length, l, decreases while their cross-sectional area, A, increases. The total number of times that the current circles the axis, N, remains constant. When using rubber tubes and air for the inside of the solenoid, the magnetic permeability of the core can be assumed to remain constant at the level of vacuum (4*π x10^-7).
Neumann Formula
Another way of calculating the inductance of the Smart Braid is through the Neumann Formula. If we assume that the current-carrying wires are very thin, and there are no sharp corners in the circuit, we can use a double curve integral to calculate the inductance. The core element of the Neumann Formula is the expression that is summed over the course of the integral.
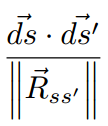
The dot product in this expression shows us that fiber segments that are aligned have a positive effect on the overall inductance of the circuit. This effect is inversely proportional to the distance between the segments. If the current in the segments flows in opposite directions, the effect on the inductance is negative.
We created a tool for calculating inductance via the Neumann formula available through the MATLAB File Exchange.
Inductance Measuring Techniques
Two off-the-shelf inductance measurement techniques are described below. The first uses a commercially available LCR meter. The second method is much less expensive but more difficult to implement.
NI PXI-4072 FlexDMM and LCR Meter
This device permits inductance to be measured at up to 40 times per second. It works by comparing the magnitude of the impedance at high and low frequencies. It requires an NI PXI chassis to function. We found that this device works well when the resistance of the braid is low. Because the excitation frequency of this sensor is relatively low (30 kHz), large electrical resistance in the Smart Braid causes the meter to malfunction. The large, 22 AWG wire actuators we tested had sufficiently low resistance.
TI LDC, Inductance to Digital Converters
These chips allow one to measure inductance very quickly (think kHz). They also comes with handy evaluation modules. The chips requires that the Smart Braid be wired in parallel with a capacitor. This parallel combination creates a resonant tank circuit with a natural frequency that varies with the changing inductance. The capacitor needs to be selected so that the natural frequency is within the specs of the chip and so that the damping ratio of the tank circuit is very low.
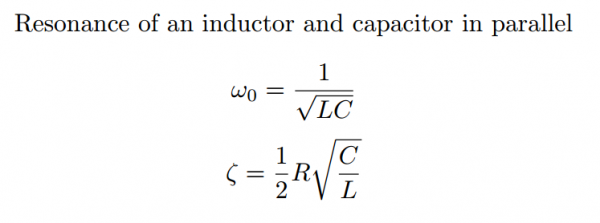
Stress and Resistance Considerations
Smart Braids need to be designed to bear the high-stresses of pressurized actuation and have low resistance. The wires that make up the braid also need to be able to withstand repeated bending and cyclic stress. For both methods of inductance measurement that we present, high circuit resistance (and relatively low inductance values) can make the measurement of inductance difficult. For these reasons, the ideal wire material would probably be thinly-insulated, stranded aluminum wire. Aluminum has both high conductivity and high tensile strength. Due to the limited commercial availability of aluminum wire, however, we use copper wire in our experiments.
The stress in the wires can be calculated using an equation presented by Davis and Caldwell.
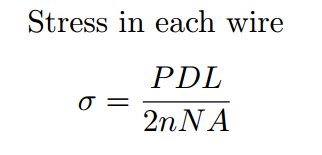
P is the pressure in the actuator, D is the diameter, L is the length, n is the number of turns each helix makes around the long axis, N is the total number of helices, and A is the cross-sectional area of the wire.

