Analytical
| The sensors consist of liquid metal channels embedded in elastomer. When the sensor is stretched, the elastomer deforms, lengthening in the direction of stretch and contracting transversely. This in turn deforms the channels, changing the shape of the liquid metal “wire” which creates a measurable increase in resistance. | 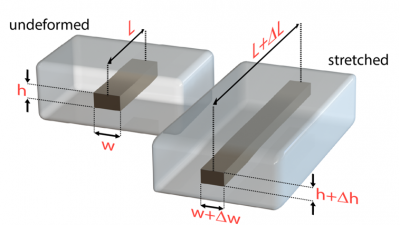 |
The change in resistance can be modeled by the following formula:
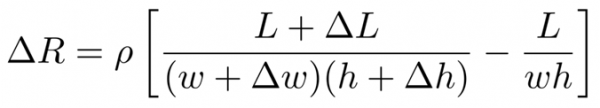
where R is resistance, ρ is resistivity (of the liquid metal), and L, w and h are the length, width and height of the channels. This formula can be further simplified using the fact that the Poisson’s ratio for incompressible materials is ν = 0.5. By defining the geometry changes in terms of strain and this ratio (ϵ = ∆L/L, ∆w = −νϵw, ∆h = −νϵh), the equation simplifies to:
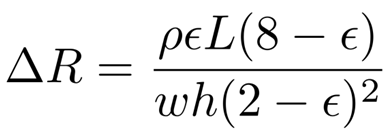
Since ρ is known (29.4 × 10−8 Ω⋅m for eGaIn) and L, w and h can be measured from the unstretched dimensions of the sensor channels, this equation gives the theoretical relationship between sensor strain and resistance change.
