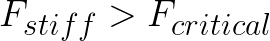In this section, we present some of the physical principles that explain the behavior and mechanical properties of Laminar Jamming Structures when jammed and unjammed. We also provide physical equations that can guide design decisions for the fabrication of LJS. Lastly, we provide a design example of a variable-stiffness problem and some relations between structural characteristics and damping ability.
Stiffness Calculation
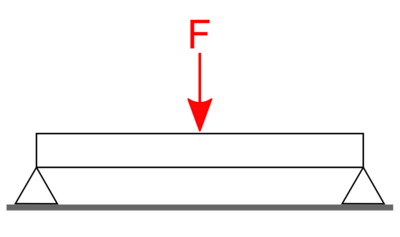 By definition, stiffness is the measurement of the resistance to deformation. In a regular 3-point bending test setup as the one shown on the left, stiffness can be calculated by the relation Applied Load / Deflection, as given in the following formula:
By definition, stiffness is the measurement of the resistance to deformation. In a regular 3-point bending test setup as the one shown on the left, stiffness can be calculated by the relation Applied Load / Deflection, as given in the following formula:
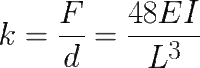
where k = stiffness, F = applied load, d = deflection, E = Young's modulus, L = Distance between supports and I = area moment of inertia.
For an unjammed Laminar Jamming Structure, the moment of inertia is calculated considering that each layer is completely independent, whereas, for a jammed LJS, we can consider that the layers are fully coupled.

This difference in moments of inertia leads to a radically different calculation of stiffness for jammed (kj) and unjammed (ko) structures, in which the ratio between the two (which is also known as the range) is n2.
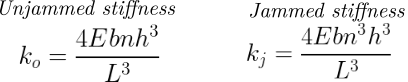
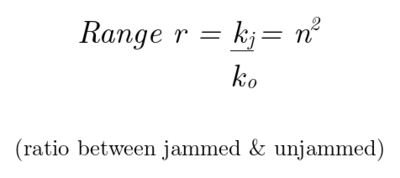
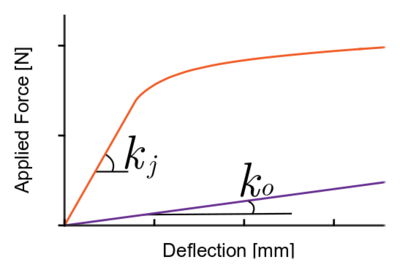
As it can be seen from the image below, the stiffness of the LJS can be also calculated from the slopes of the linear regions in the force-deflection curve.
Yield Point and Critical Force
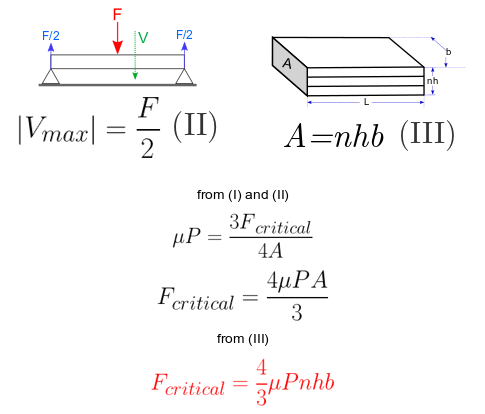
The yield point for a Laminar Jamming Structure is defined as the point after which any deflection will cause the layers of the structure to slip with respect to one another. Therefore it is proportional to the coefficient of friction between layers. Because the structure slips due to shear, the yield occurs when the shear stress in the structure equals the maximum shear stress (τmax) that can be supported by friction (μP). Note that the maximum shear stress in the rectangular beam is 3V/2A. After yield, the structure becomes much less stiff.

Design LJS for Variable Stiffness
If I load my sample with Fstiff Newtons applied in the center and don't want the structure to deflect more than Dstiff mm in the jammed state, I should pick kj such that:

If I load my sample with Fcompliant Newtons and want it to deflect by at least Dcompliant in the unjammed state, I should pick ko such that:
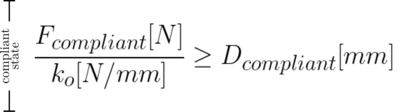
Make sure your load Fstiff does not exceed Fcritical, as the stiffness decreases after yield, as mentioned earlier.
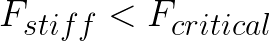
Please note that these calculations were made with the assumption that the applied load was done under a 3-point bending test. You may use/derive different formulas for different loading conditions.
Design LJS for Variable Damping
Damping corresponds to the amount of energy dissipated by your structure. There is not a simple analytical expression to calculate it according to your structure, but damping should scale linearly with μ, P and n.
If you want to use your Laminar Jamming Structure as an energy dissipation mechanism, make sure that the structure is jammed and that the forces applied are above the yield point.