Theoretical studies and models on the single module and on the manipulator have been conducted. In this section, the Finite Element Analysis, the theoretical stiffness evaluation and a mechanical model are reported.
FEA simulation
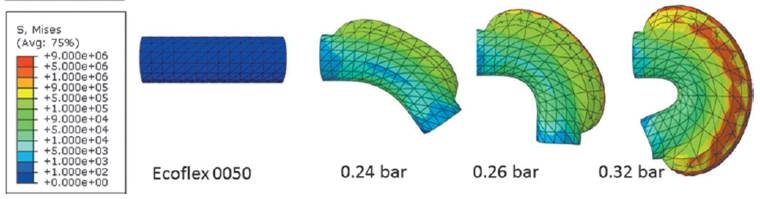
FEA simulations of the module when one chamber is actuated are reported in Elsayed et al. Results relative to the single module can be analytically extended to the multi-module configuration.
Stiffness Evaluation
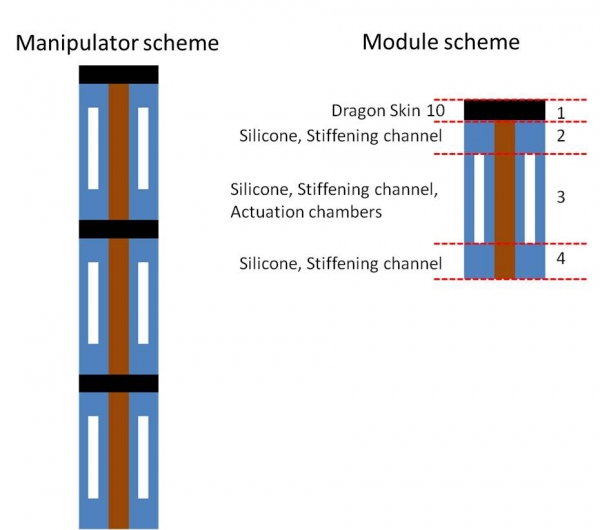
In De Falco et al., the soft manipulator has been studied in terms of variable stiffness. The stiffness has been theoretically calculated for a 10% compression in axial direction of the manipulator. Reuss model and composite materials properties have been applied to the module scheme and then extended to the manipulator.
From Reuss model we know that:
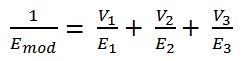
where V1,2,3,4 are the volume fractions of Part 1,2,3,4 indicated in Module scheme and E1,2,3,4 are the respective Young's moduli. The elastic moduli of the single components are:

For the composite parts of the module the elastic moduli are given by:
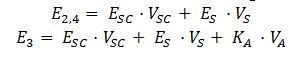
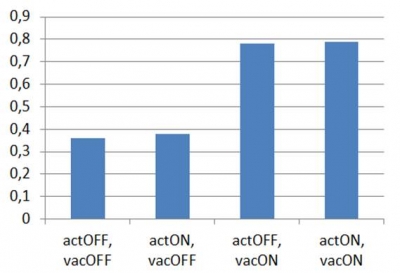
- actON, vacON: all 9 chambers are actuated with the same pressure (650 mbar), granular jamming is simultaneously activated in all 3 modules (980 mbar vacuum pressure).
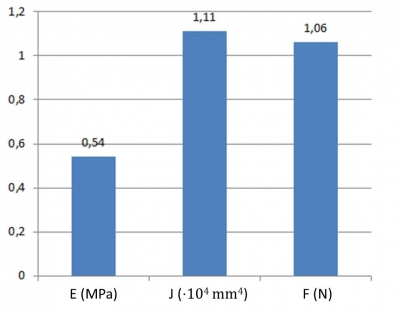
The following graph shows the results relative to the theoretical stiffness evaluation.
Mechanical model

In this case, the mechanical behaviour of the module can be studied taking into account the low length/diameter ratio of the module for which:

Elastic modulus is calculated as already explained above, using Reuss model and composite materials rules. The area moment of inertia is calculated considering the crossing section of the module and the sum of the single moments due to the different components of the section:
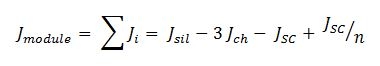
where sil indicates the silicone module, ch the actuation chambers, SC the stiffening channel and n the ratio between EGJ and Esil.
The shear modulus is calculated as:
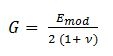
where Poisson value, ν, is 0.5, typical of rubber materials. For the shear factor, χ, we use 10/9 that is relative to circle section.
If you know the maximum imposed deflection, you can calculate the maximum force, because the other parameters of the equation are geometric so you already know them. In the following graphs, the values of the Young's modulus, the moment of inertia and the maximum force are reported. They have been calculated considering the data discussed before and a deflection of 10 mm. The module is 50 mm in length and 25 mm (without sheath) in diameter. When this model is applied to the manipulator (three modules), the different length has to be considered.