Analytical
There are several existing analytical models for McKibbens/PAMs, which vary in complexity as well as closeness to experimental results. The most widely cited model is by Chou and Hannaford, a static model assuming an ideal actuator that is cylindrical (no tapering at the ends) and ignores friction and bladder wall thickness/elasticity. Using conservation of energy principles and braid geometry, the following relationship between force, pressure, and braid angle is derived:
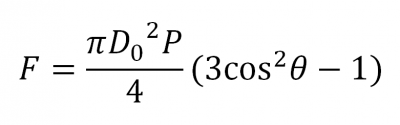
Where D0 is the mesh diameter when braid angle is 90°. Setting F=0 and solving for braid angle yields 54.7 degrees, the neutral/“magic” angle at which the maximal contraction is reached.
The Chou and Hannaford model has been found to deviate up to 15% from experimental results. Some models take into account factors such as friction between braid fibers, reducing the deviation from experimental results to 5% at the cost of greatly increased complexity.
Finite Element
To model the response of the actuators to an increase in pressure, without the need for a detailed model of the braided mesh, temperature and orthotropic coefficients of thermal expansion can be used to simulate the anisotropic strain response of these actuators.
This is useful for modeling devices where the actuators are integrated into other materials, such as in the cardiac simulator case study where actuators were arranged and embedded inside an elastomeric matrix. Actuators were assigned an experimentally derived modulus of 1.78 MPa and orthotropic thermal expansion coefficients according to experimentally derived strains that were negative in the longitudinal direction and positive in the radial direction for a positive change in pressure.
